مسابقه تلویزیونی هوشیار – قسمت ۴۷

این دنباله با اعداد \(3\) و \(6\) شروع می‌شود و اعداد بعدی به‌صورت زیر به‌دست می‌آیند:
\[\begin{aligned}&3+6{\,-\,\color{red}1}=8\\&6+8{\,-\,\color{red}2}=12\\&8+12{\,-\,\color{red}3}=17\\&12+17{\,-\,\color{red}4}=25\\&17+25{\,-\,\color{red}5}=37\\&25+37{\,-\,\color{red}6}=56.\end{aligned}\]بنابراین، گزینهٔ ۴ درست است.

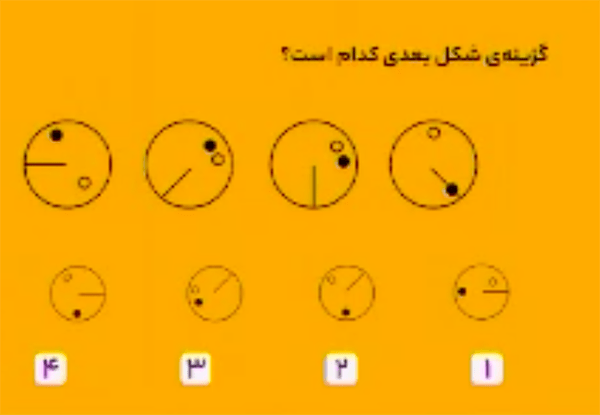
در هر مرحله،
\(\bullet\) شعاع دایره \(45\) درجه پادساعتگرد می‌چرخد؛
\(\bullet\) دایرهٔ توپر \(45\) درجه ساعتگرد می‌چرخد؛
\(\bullet\) و دایرهٔ توخالی \(45\) درجه پادساعتگرد می‌چرخد.

بنابراین، گزینهٔ ۴ درست است.

برای تولید این دنباله، ابتدا اعداد
\[\begin{aligned}&1\times1=1\\&2\times2=4\\&3\times3=9\\&4\times4=16\\&5\times5=25\\&6\times6=36\\&7\times7=49\\&8\times8=64\end{aligned}\] را می‌نویسیم. سپس، هر عدد را با عدد قبلی‌اش جمع می‌زنیم:
\[\begin{aligned}&4+1=5\\&9+5=14\\&16+14=30\\&25+30=55\\&36+55=91\\&49+91=140\\&64+140=204.\end{aligned}\]بنابراین، گزینهٔ ۴ درست است.

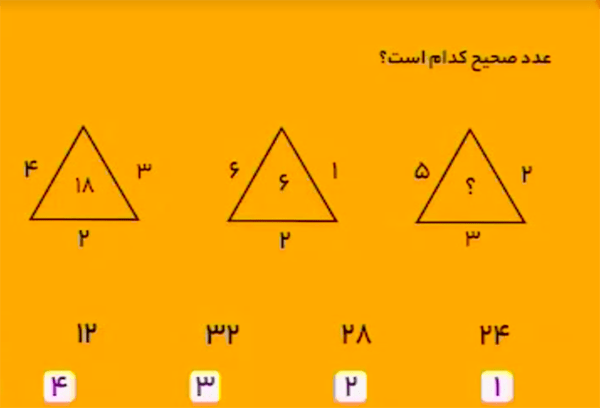
در شکل سمت چپ، عدد وسط با قانون زیر، اعداد اطراف مثلث ساخته می‌‌شود:
\[3\times2\times4-6=24-6=18.\]
در شکل میانی نیز با همین قانون می‌توان عدد وسط را به‌دست آورد:
\[1\times2\times6-6=12-6=6.\]
پس در شکل سمت راست داریم:
\[2\times3\times5-6=30-6=24.\]بنابراین، گزینهٔ ۱ درست است.

گزینهٔ ۴ درست است.

دنبالهٔ داده شده از دو دنباله تشکیل شده است:
\[{\color{blue}1},{\color{red}2} ,{\color{blue}0},{\color{red}3} ,{\color{blue}-1},{\color{red}4}\] دنبالهٔ قرمز با عدد \(2\) شروع می‌شود و هر عدد بعدی، \(1\) واحد از عدد قبلی‌اش بزرگ‌تر است.
دنبالهٔ آبی با عدد \(1\) شروع می‌شود و هر عدد بعدی \(1\) واحد از عدد قبلی‌اش کوچک‌تر است. پس به‌جای علامت سؤال باید عدد \(-2\) را قرار داد.
بنابراین، گزینهٔ ۱ درست است.

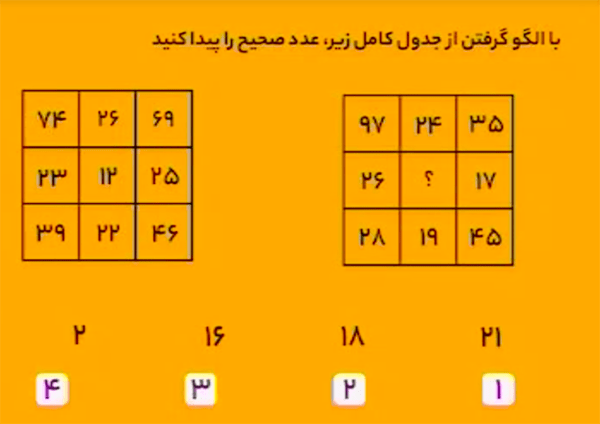
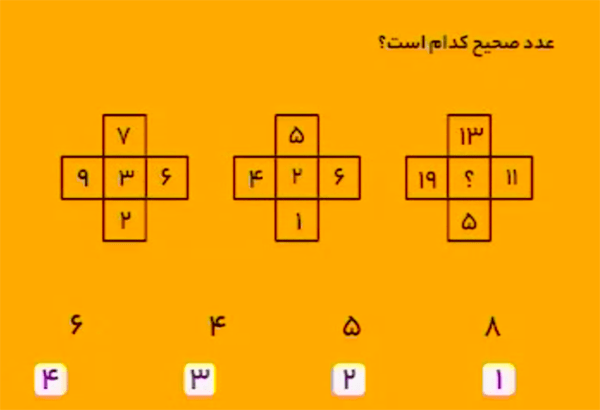
در هر ستون، ابتدا مجموع رقم‌های عدد بالا و مجموع رقم‌های عدد پایین را به‌دست آورید. سپس، اگر اعداد به‌دست آمده را باهم جمع بزنید، حاصل، عدد میانی آن ستون خواهد بود. برای مثال، در ستون سمت چپ داریم:
\[\begin{aligned}&7+4=11\\&3+9=12\\&11+12=23.\end{aligned}\]
بنابراین، در ستون میانی جدول سمت راست داریم:
\[\begin{aligned}&2+4=6\\&1+9=10\\&6+10=16.\end{aligned}\] بنابراین، گزینهٔ ۳ درست است.

در شکل سمت چپ داریم:
\[(7+9+2+6)\div8=24\div8=3.\]
در شکل میانی داریم:
\[(5+4+1+6)\div8=16\div8=2.\]
در شکل سمت راست خواهیم داشت:
\[(13+19+5+11)\div8=48\div8=6.\] بنابراین، گزینهٔ ۴ درست است.

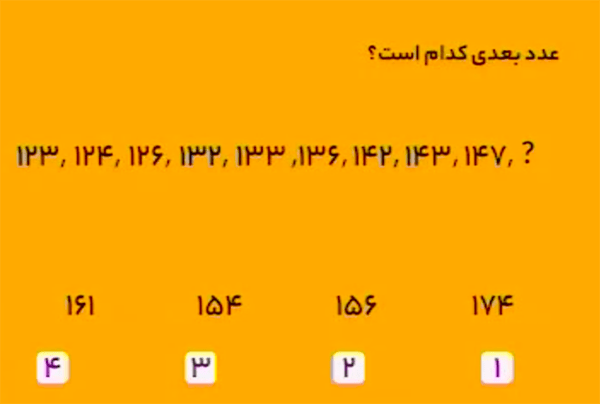
این دنباله با عدد \(123\) شروع می‌شود و اعداد بعدی به‌ترتیب از حاصل‌جمع عدد قبلی و رقم صدگان، دهگان، و یکان آن عدد، به‌صورت زیر به‌دست می‌آیند:
\[\begin{aligned}&{\color{blue}1}23+{\color{blue}1}=124\\&1{\color{blue}2}4+{\color{blue}2}=126\\&12{\color{blue}6}+{\color{blue}6}=132\\&{\color{blue}1}32+{\color{blue}1}=133\\&1{\color{blue}3}3+{\color{blue}3}=136\\&13{\color{blue}6}+{\color{blue}6}=142\\&{\color{blue}1}42+{\color{blue}1}=143\\&1{\color{blue}4}3+{\color{blue}4}=147\\&14{\color{blue}7}+{\color{blue}7}=154.\end{aligned}\]