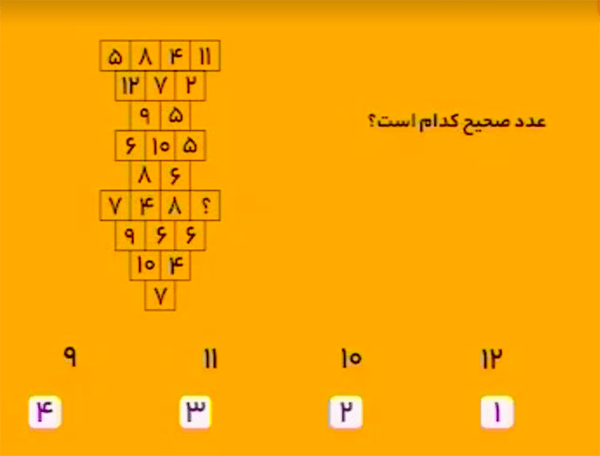
در جدول داده شده،
\(\bullet\) مجموع اعداد سطرهای چهار عددی برابر \(28\)،
\(\bullet\) مجمع اعداد سطرهای سه عددی برابر \(21\)،
\(\bullet\) مجموع اعداد سطرهای دو عددی برابر \(14\)،
\(\bullet\) و مجموع اعداد سطرهای یک عددی برابر \(7\) است.
پس بهجای علامت سؤال باید عدد \(9\) را قرار داد.
بنابراین، گزینهٔ ۴ درست است.
دنبالهٔ داده شده با عدد \(7\) و \(8\) شروع میشود و اعداد بعدی از مجموع دو عدد قبلی بهاضافهٔ شمارهٔ جایگاه عدد قبلی، بهدست میآید:
\[\begin{aligned}&7+8+{\color{red}2}=17\\&8+17+{\color{red}3}=28\\&17+28+{\color{red}4}=49\\&28+49+{\color{red}5}=82\\&49+82+{\color{red}6}=137\\&82+137+{\color{red}7}=226.\end{aligned}\]بنابراین، گزینهٔ ۴ درست است.
اعداد داده شده را بهصورت زیر بنویسید و هرکدام را نشاندهندهٔ ساعتی از روز در نظر بگیرید:
\[\begin{aligned}&125\rightarrow1:25\\&150\rightarrow1:50\\&215\rightarrow2:15\\&240\rightarrow2:40\\&305\rightarrow3:05\\&330\rightarrow3:30\\&355\rightarrow3:55\end{aligned}\] یعنی دنبالهٔ داده شده با ساعت \(1\) و \(25\) دقیقه شروع میشود و هر عدد بعدی، \(25\) دقیقه از عدد قبلی جلوتر است. پس بهجای علامت سؤال باید عدد \(420\)، یا همان \(4\) و \(20\) دقیقه، را قرار داد.
بنابراین، گزینه ۳ درست است.
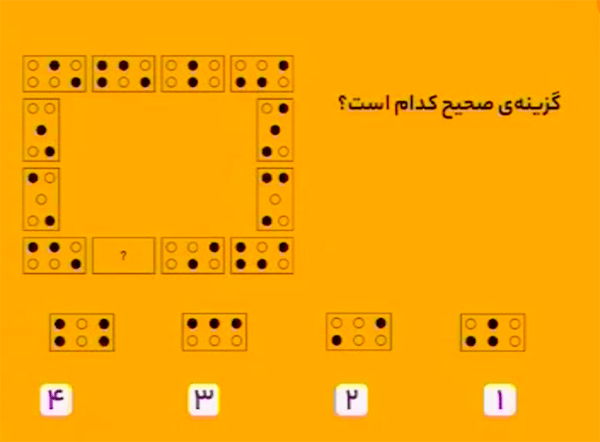
هر شکل را، بهصورت زیر، با شکل مقابلش یک جفت در نظر میگیریم.

در هر جفت، رنگ دایرهها برعکس همدیگر هستند؛ یعنی دایرههای توپر به دایرههای توخالی تبدیل میشوند و دایرههای توخالی به دایرههای توپر.
بنابراین، گزینهٔ ۴ درست است.
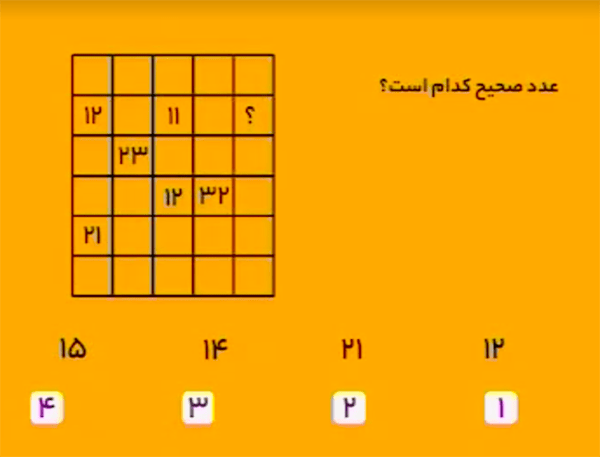
یکان هر عدد دورقمی تعداد خانههای خالی پایین آن عدد، و دهگان آن، تعداد خانههای خالی بالای آن عدد را نشان میدهد. پس بهجای علامت سؤال باید عدد \(15\) را قرار داد.
بنابراین، گزینهٔ ۴ درست است.
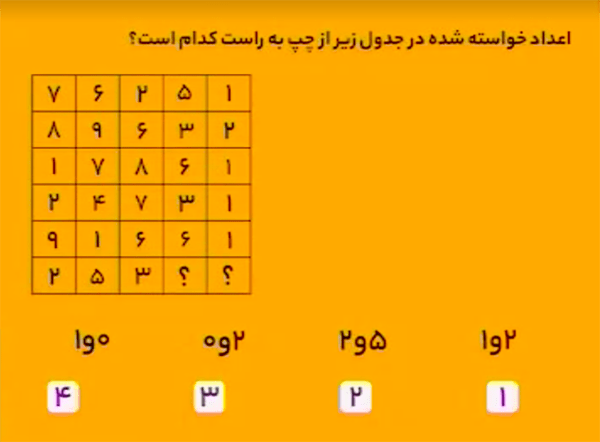
در سطر اول،
\[7+6+2=15.\] یکان \(15\) در خانهٔ چهارم سطر اول و دهگانش در خانهٔ پنجم سطر اول قرار داده شده است.
در سطر دوم،
\[8+9+6=23.\] یکان \(23\) در خانهٔ چهارم سطر دوم و دهگانش در خانهٔ پنجم سطر دوم قرار داده شده است.
در سطرهای دیگر نیز همین قانون برقرار است.
در سطر آخر،
\[2+5+3=10.\] پس در خانهٔ چهارم و پنجم سطر آخر، بهترتیب باید اعداد \(0\) و \(1\) را قرار داد.
بنابراین، گزینهٔ ۴ درست است.
ابتدا فرض کنید که عدد علامت سؤال بهصورت \(abc\) باشد. حالا، همه ارقام دنباله را پشت سرهم مینویسیم:
\[272931{\color{red}abc}537394143\] و دورقم دورقم آنها را جدا میکنیم:
\[27,29,31,{\color{red}ab},{\color{red}c}5,37,39,41,43.\] پس دنبالهای داریم که با عدد \(27\) شروع شده است و هر عدد \(2\) واحد از عدد قبلیاش بزرگتر است. در نتیجه، این دنباله اینگونه است:
\[27,29,31,{\color{red}33},{\color{red}3}5,37,39,41,43.\] بنابراین، گزینهٔ ۲ درست است.
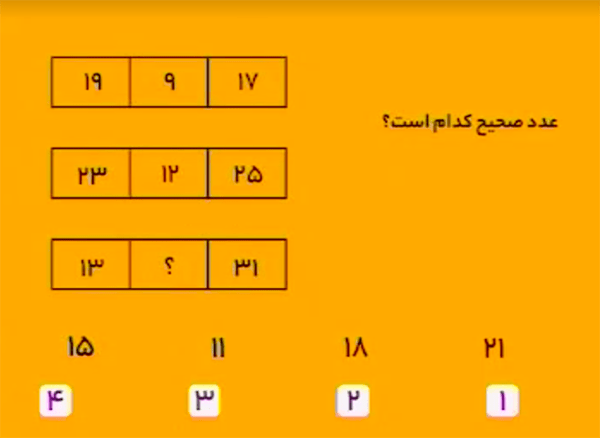
در هر سطر، عدد وسط یکچهارم مجموع دو عدد سمت چپ و راست است:
\[\begin{aligned}&(19+17)\div4=36\div4=9\\&(23+25)\div4=48\div4=12\\&(13+31)\div4=44\div4=11.\end{aligned}\]بنابراین، گزینهٔ ۳ درست است.
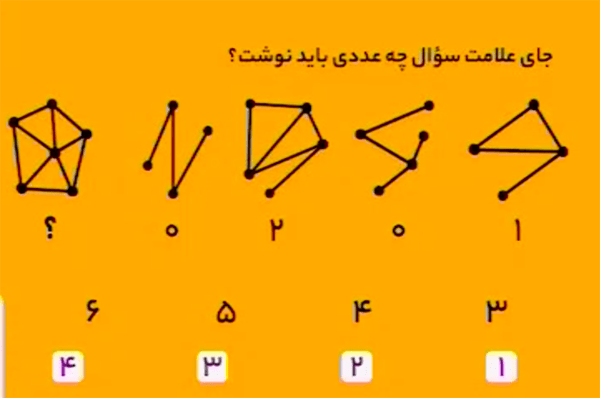
زیر هر شکل تعداد مثلثهای آن شکل نوشته شده است.
بنابراین گزینهٔ ۳ درست است.












ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️