مسابقه تلویزیونی هوشیار – قسمت ۵۰

برای ساختن هر عدد از عدد قبلی، ابتدا ترتیب ارقام را برعکس می‌کنیم و سپس، \(1\) واحد به رقم قرمزرنگ اضافه می‌شود:
\[\begin{aligned}&964{\color{red}2}1\rightarrow1{\color{red}2}469\rightarrow1{\color{red}3}469\\&1{\color{red}3}469\rightarrow964{\color{red}3}1\rightarrow964{\color{red}4}1\\&964{\color{red}4}1\rightarrow1{\color{red}4}469\rightarrow1{\color{red}5}469\\&1{\color{red}5}469\rightarrow964{\color{red}5}1\rightarrow964{\color{red}6}1.\end{aligned}\] بنابراین، گزینهٔ ۳ درست است.

در هر سطر، از چپ به راست، عدد اول و سوم را یک عدد دورقمی و عدد دوم و چهارم را نیز یک عدد دورقمی در نظر بگیرید. حاصل‌جمع این دو عدد دورقمی برابر است با عدد پنجم همان سطر. برای مثال، در سطر اول،
\[84+22=106.\] در سطر آخر داریم:
\[91+37=128.\] بنابراین، گزینهٔ ۳ درست است.

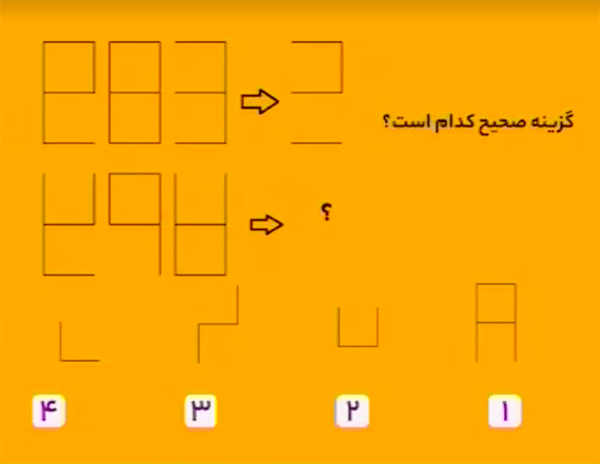
سه شکل سمت چپ را روی‌هم می‌اندازیم. اگر سه‌خط روی‌هم بیفتند، آن خط‌ها در شکل سمت راست ظاهر می‌شوند.
بنابراین، گزینهٔ ۲ درست است.

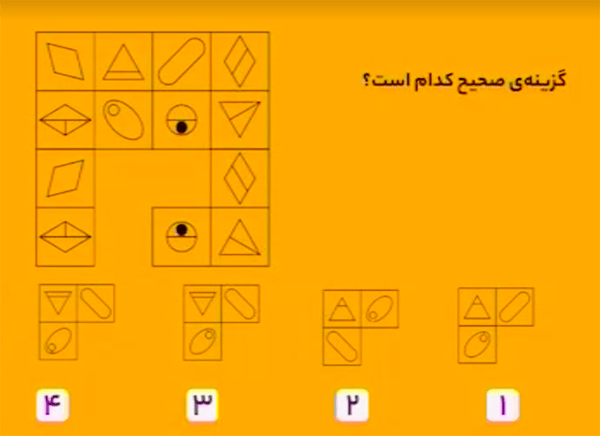
در هر ستون، از بالا به پایین، اگر شکل اول را ۱۸۰ درجه دوران دهیم، شکل سوم به‌دست می‌آید. همچنین، اگر شکل دوم را ۱۸۰ درجه دوران دهیم، شکل چهارم به‌دست می‌آید.
بنابراین، گزینهٔ ۴ درست است.

در هر عدد، یکان و صدگان را به‌هم می‌چسبانیم تا یک عدد دورقمی به‌دست آید. برای مثال، با چسباندن یکان و صدگان \(368\) به یکدیگر، عدد \(38\) به‌دست می‌آید. حالا، اگر \(38\) را با \(368\) جمع بزنیم، عدد بعدی، یعنی \(406\) به‌دست می‌آید. برای بقیهٔ اعداد نیز همین قانون را به‌کار می‌بریم:
\[\begin{aligned}&{\color{blue}4}0{\color{blue}6}+{\color{blue}46}=452\\&{\color{blue}4}5{\color{blue}2}+{\color{blue}42}=494\\&{\color{blue}4}9{\color{blue}4}+{\color{blue}44}=538\\&{\color{blue}5}3{\color{blue}8}+{\color{blue}58}=596.\end{aligned}\]بنابراین، گزینهٔ ۳ درست است.

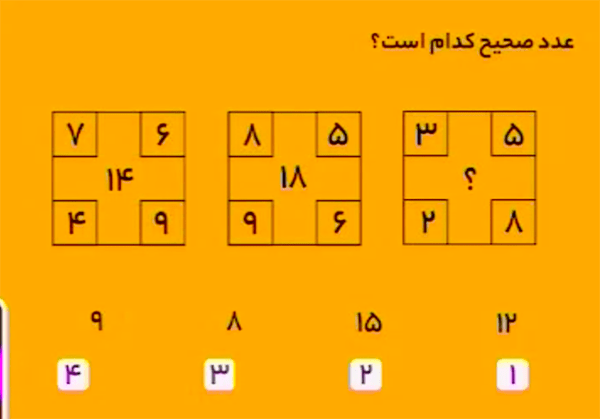
در شکل سمت چپ داریم:
\[7+9+4-6=14.\] در شکل میانی داریم:
\[8+9+6-5=18.\] در شکل سمت راست داریم:
\[3+2+8-5=8.\]بنابراین، گزینهٔ ۳ درست است.

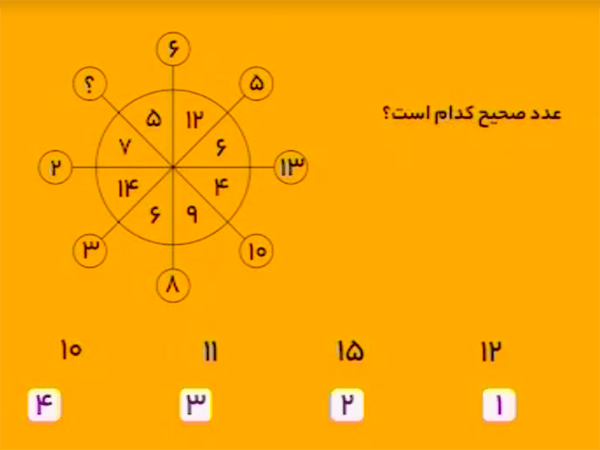
به اعداد \(6\) و \(5\) و \(12\) دقت کنید.

در مقابل این اعداد، \(8\) و \(9\) و \(6\) قرار دارند؛ و
\[6+5+12=8+9+6.\]

به اعداد \(5\) و \(12\) و \(6\) دقت کنید. در مقابل این اعداد، \(3\) و \(6\) و \(14\) قرار دارند؛ و
\[5+12+6=3+6+14.\]

با همین قانون، باید داشته باشیم:
\[10+4+9=?+7+5.\] پس به‌جای علامت سؤال باید عدد \(11\) را قرار داد.
بنابراین، گزینهٔ ۳ درست است.

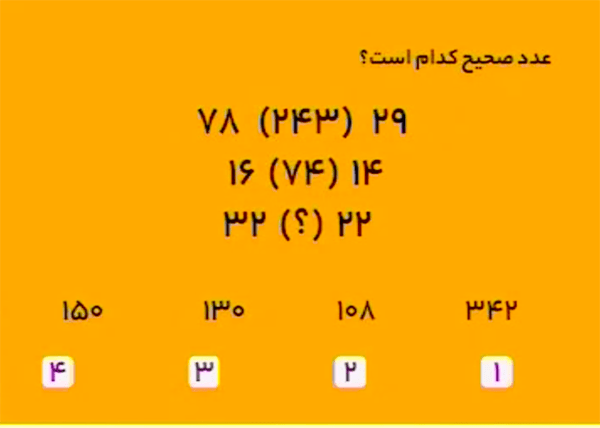
در هر سطر، دوبرابر عدد سمت چپ را با سه‌برابر عدد سمت راست جمع بزنید تا عدد میانی به‌دست آید:
\[\begin{aligned}&2\times78+3\times29=156+87=243\\&2\times16+3\times14=32+42=74\\&2\times32+3\times22=64+66=130.\end{aligned}\]بنابراین، گزینهٔ ۳ درست است.

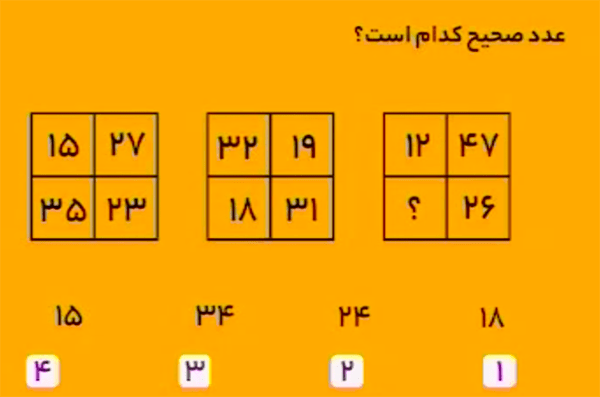
حاصل‌جمع چهار عدد مربع سمت چپ و مربع میانی برابر \(100\) است.
\[\begin{aligned}&15+27+23+35=100\\&32+19+31+18=100.\end{aligned}\]برای اینکه حاصل‌جمع چهار عدد مربع سمت راست نیز برابر \(100\) شود، باید به‌جای علامت سؤال عدد \(15\) را قرار داد.
بنابراین، گزینهٔ ۴ درست است.

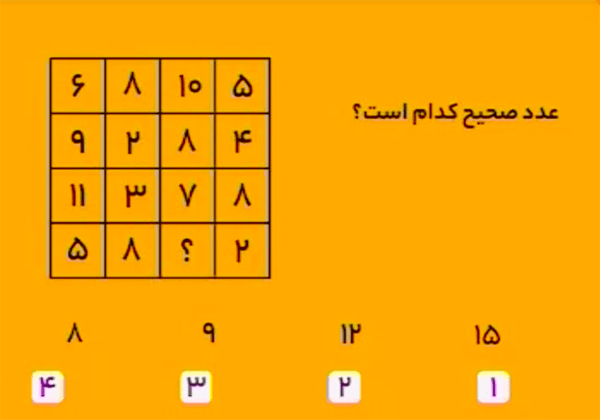
در سطر اول:
\[\begin{aligned}&6+8=14\\&10+5=15\end{aligned}\] در سطر دوم:
\[\begin{aligned}&9+2=11\\&8+4=12\end{aligned}\] در سطر سوم:
\[\begin{aligned}&11+3=14\\&7+8=15\end{aligned}\]
همان‌طور که مشاهده می‌کنیم حاصل‌جمع اعداد اول و دوم هر سطر، از حاصل‌جمع اعداد سوم و چهارم همان سطر، \(1\) واحد کمتر است. همین قانون در مورد ستون‌ها نیز درست است. پس به‌جای علامت سؤال باید عدد \(12\) را قرار دهیم تا در سطر چهارم داشته باشیم:
\[\begin{aligned}&5+8=13\\&{\color{red}12}+2=14\end{aligned}\] و در ستون سوم داشته باشیم:
\[\begin{aligned}&10+8=18\\&7+{\color{red}12}=19.\end{aligned}\]بنابراین، گزینهٔ ۲ درست است.

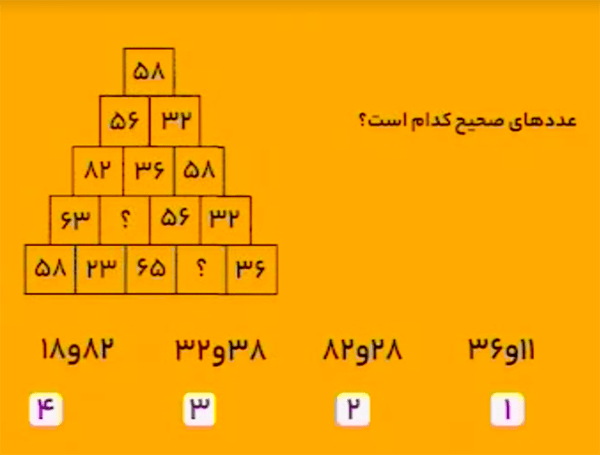
دنبالهٔ \[5,8,2,3,6\] را در نظر بگیرید. از خانهٔ بالای جدول داده شده شروع به حرکت کنید و در هر خانه دورقم از این دنباله را قرار دهید. در سطر اول دورقم \(58\) قرار گرفته است. وقتی یک سطر تمام می‌شود به سطر بعدی می‌رویم. در سطر دوم، اعداد این دنباله را از راست به چپ قرار می‌‌دهیم. هروقت اعداد دنباله تمام می‌شود، دوباره آن را تکرار می‌کنیم.
اگر از بالای جدول شروع به حرکت کنید و اعداد را پشت‌سر هم بخوانید،
\[5,8,2,3,6\] تکرار می‌شود.

پس در مربع خالی سطر چهارم عدد \(28\) و در مربع خالی سطر پنجم عدد \(82\) را باید قرار داد.
بنابراین، گزینهٔ ۲ درست است.