مسابقه تلویزیونی هوشیار – قسمت ۵۱

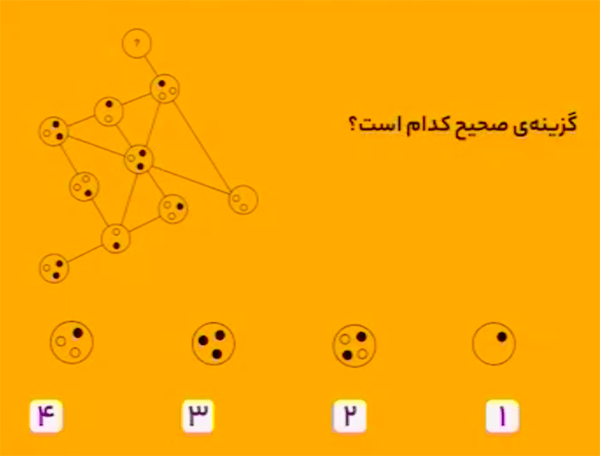
روی هر پاره‌خط سه‌‌تا دایره وجود دارد که مجموع دایره‌های توخالی داخل این سه دایره برابر \(4\) و مجموع دایره‌های توپر داخل این سه دایره نیز برابر \(4\) است. بنابراین، گزینهٔ ۳ درست است.

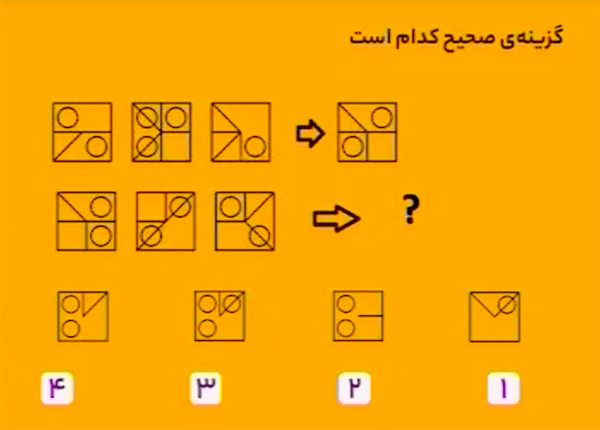
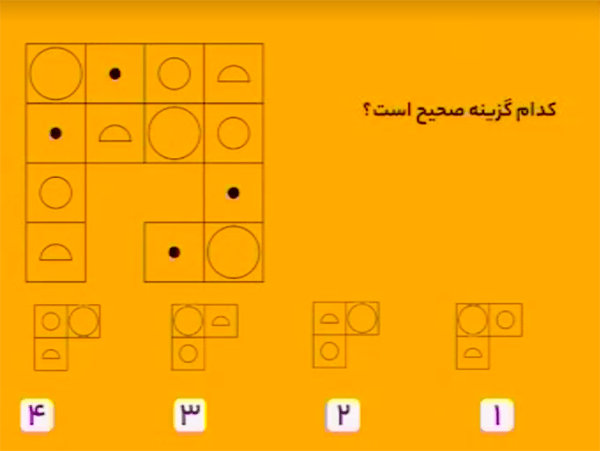
از روی‌هم انداختن سه شکل سمت چپ، با قانون‌های زیر، شکل سمت راست به‌دست می‌آید:
\(\bullet\) اگر \(2\) دایره روی‌هم بیفتند، حذف می‌شوند.
\(\bullet\) اگر دقیقاً \(2\) خط روی‌هم بیفتند، در شکل سوم دیده می‌شوند؛ در غیر‌‌این‌صورت خط‌ها حذف می‌شوند.
بنابراین، گزینهٔ ۴ درست است.

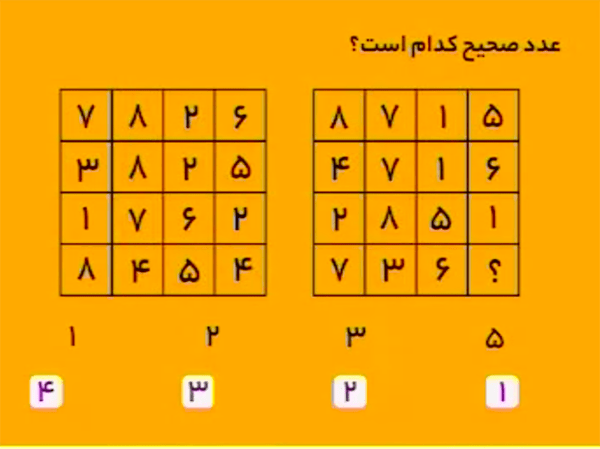
اعداد جدول سمت راست به‌ترتیب از اعداد متناظر آن در جدول سمت چپ، با قانون زیر، به‌دست می‌آیند:
\(\bullet\) به اعداد فرد یکی اضافه می‌شود و از اعداد زوج یکی کم می‌شود.

برای مثال، اعداد سطر اول جدول سمت چپ \(7\)، \(8\)، \(2\)، و \(6\) هستند. با قانون گفته شده، اعداد سطر اول جدول سمت راست را به‌صورت زیر می‌سازیم:
\[\begin{aligned}&7+1=8\\&8-1=7\\&2-1=1\\&6-1=5.\end{aligned}\]همان‌طور که می‌بینید، اعداد سطر اول جدول سمت راست، \(8\)، \(7\)، \(1\)، و \(5\) هستند. پس به‌جای علامت سؤال باید \[4-1=3\]را قرار داد.
بنابراین، گزینهٔ ۲ درست است.

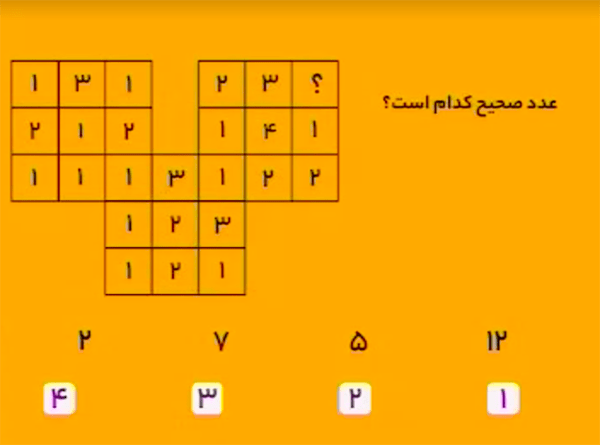
از چپ به راست، اعداد داخل هریک از ستون‌ها را جمع می‌زنیم:
\[\begin{aligned}1+2+1&=4\\3+1+1&=5\\1+2+1+1+1&=6\\3+2+2&=7\\2+1+1+3+1&=8\\3+4+2&=9.\end{aligned}\]پس حاصل‌جمع ستون آخر باید برابر \(10\) باشد. در نتیجه، به‌جای علامت سؤال باید \(7\) را قرار داد.
بنابراین، گزینهٔ ۳ درست است.

در جدول داده شده، هر شکل باید دقیقاً یک‌بار در هر سطر و هر ستون ظاهر شود.
بنابراین، گزینهٔ ۳ درست است.

(دربارهٔ مربع‌های لاتین تحقیق کنید.)

دنبالهٔ داده شده با عدد \(1\) شروع می‌شود و هریک از اعداد بعدی، \(1\) واحد کمتر از \(3\) برابر عدد قبلی است.
\[\begin{aligned}&2=3\times1-1\\&5=3\times2-1\\&14=3\times5-1\\&41=3\times14-1.\end{aligned}\]پس به‌جای علامت سؤال باید
\[3\times41-1=123-1=122\] را قرار داد.
بنابراین، گزینهٔ ۲ درست است.

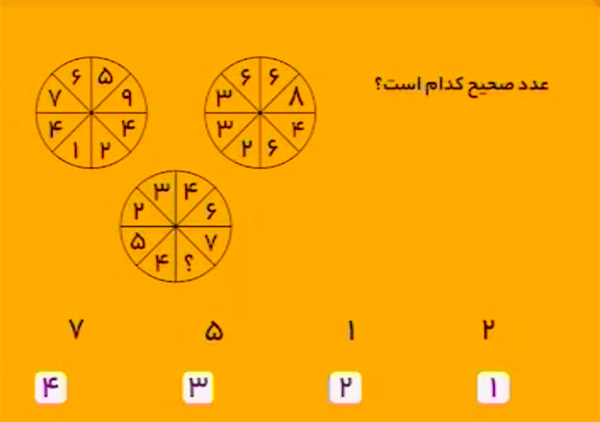
اعداد دایرهٔ بالا سمت چپ را می‌توان به‌صورت دو دسته عدد دورقمی نوشت:
\[\begin{aligned}&76,24\\&59,41\\\end{aligned}\] که حاصل‌جمع هر دسته برابر \(100\) است.

اعداد دایرهٔ بالا سمت راست را نیز می‌توان با قانونی مشابه، به‌صورت دو دسته عدد دورقمی نوشت:
\[\begin{aligned}&36,64\\&68,32\end{aligned}\] که حاصل‌جمع هر دسته برابر \(100\) است.

در دایرهٔ پایین هم همین قانون برای \(46,54\) برقرار است و اگر به‌جای علامت سؤال \(7\) بگذاریم، قانون برای دایرهٔ پایین هم برقرار می‌شود. چون \[23+77=100.\]

بنابراین، گزینهٔ ۴ درست است.

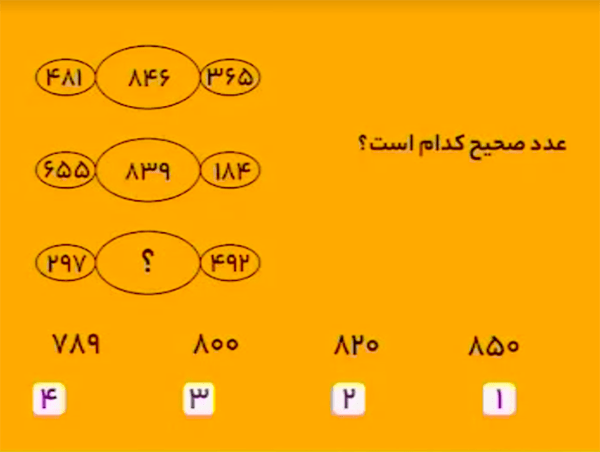
در هر سطر، حاصل‌جمع دو عدد سمت چپ و راست برابر عدد میانی است.
\[\begin{aligned}481+365&=846\\655+184&=839\end{aligned}\]پس
\[297+492=789.\]

دنبالهٔ داده شده با \(0\)، \(1\)، و \(2\) آغاز می‌شود، و هر عدد از حاصل‌جمع سه عدد قبلی‌اش به‌دست می‌آید. پس به‌جای علامت سؤال باید
\[11+20+37=68\] را قرار داد.
بنابراین، گزینهٔ ۲ درست است.

در این سؤال، باید به حروف کلمهٔ «هوشیار» دقت کنید که هرکدام از آنها چندمین حرف در الفبای فارسی هستند.
«هـ»: حرف شماره \(31\)
«و»: حرف شماره \(30\)
«ش»: حرف شماره \(16\)
«ی»: حرف شماره \(32\)
«ا»: حرف شماره \(1\)
«ر»: حرف شماره \(12\)
شمارهٔ هر حرف را به‌صورت یک دنباله می‌نویسیم:
\[31,30,16,32,1,12.\]پس به‌جای علامت سؤال باید عدد \(32\) را قرار دهیم.
بنابراین، گزینهٔ ۱ درست است.