مسابقه تلویزیونی هوشیار – قسمت ۱۵

با حروف گزینهٔ۱ واژهٔ «تن‌پرور»
با حروف گزینهٔ۲ واژهٔ «سخت‌کوش»
با حروف گزینهٔ۳ واژهٔ «خوش‌گذر»
و با حروف گزینهٔ۴ واژهٔ «همکاری» ساخته می‌شود. متضاد واژهٔ «تن‌آسا»، کلمهٔ «سخت‌کوش» است.

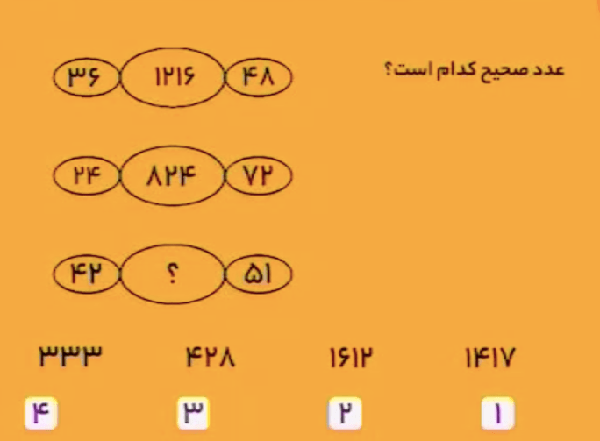
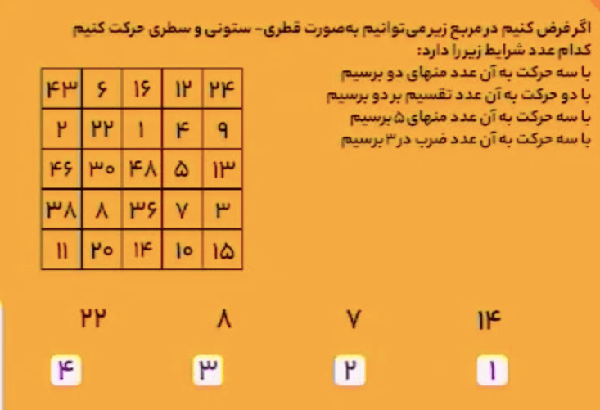
در هر سطر عدد سمت چپ و سمت راست را بر \(3\) تقسیم کنید و دو عدد به‌دست آمده را در کنارهم بگذارید تا عدد میانی آن سطر به‌دست آید.
عدد میانی سطر اول، \({\color{red}12}{\color{blue}16}\) است، زیرا:
\[\begin{aligned}&36\div3={\color{red}12}\\&48\div3={\color{blue}16}.\end{aligned}\]
عدد میانی سطر دوم، \({\color{red}8}{\color{blue}24}\) است، زیرا:
\[\begin{aligned}&24\div3={\color{red}8}\\&72\div3={\color{blue}24}.\end{aligned}\]
عدد میانی سطر سوم، \({\color{red}14}{\color{blue}17}\) است، زیرا:
\[\begin{aligned}&42\div3={\color{red}14}\\&51\div3={\color{blue}17}.\end{aligned}\]

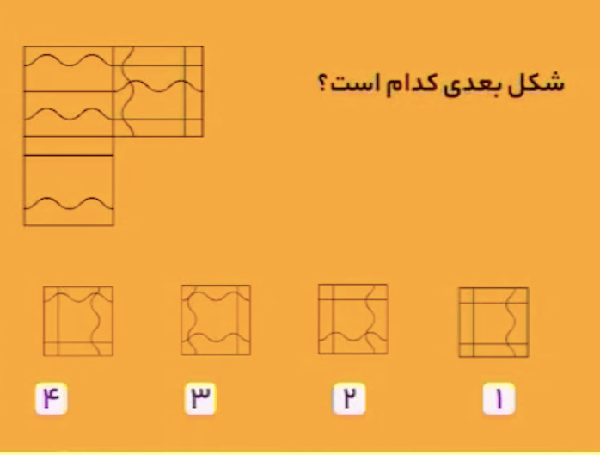
خط‌های هر مربع کوچک در مربع همسایه امتداد پیدا می‌کنند با این شرط که خطوط راست تبدیل به خطوط موجی می‌شوند، و برعکس. بنابراین، شکل زیر، پاسخ مسئله است.

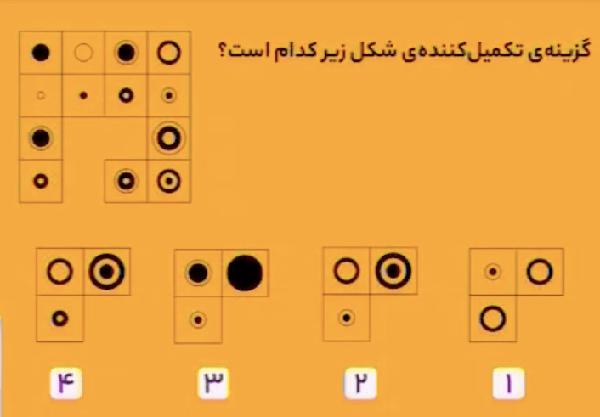
در سطرهای \(1\) و \(4\)، از چپ به راست، شکل سوم همان شکل اول است که یک دایره (حلقه) سفید دور آن رسم شده است؛ و شکل چهارم همان شکل دوم است که یک دایره (حلقه) سیاه دور آن رسم شده است.
در سطرهای \(2\) و \(3\)، از چپ به راست، شکل سوم همان شکل اول است که یک دایره (حلقه) سیاه دور آن رسم شده است؛ و شکل چهارم همان شکل دوم است که یک دایره (حلقه) سفید دور آن رسم شده است.

قانون‌های بالا برای ستون‌ها نیز برقرار است.

بنابراین، شکل زیر، پاسخ مسئله است.

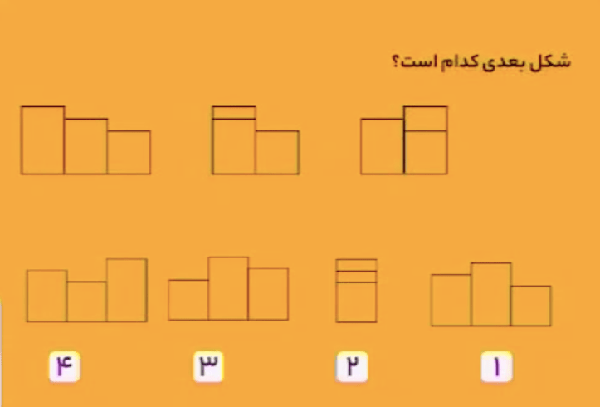
مستطیل سمت چپ شکل اول، در هر مرحله، یک واحد به سمت راست حرکت کرده است. بنابراین، شکل زیر، پاسخ مسئله است.

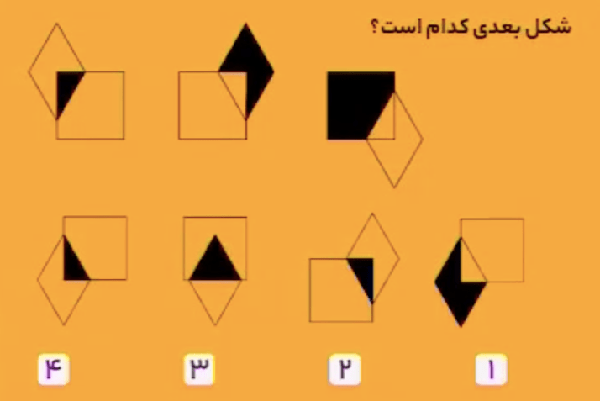
لوزی در گوشه‌های مربع به‌صورت ساعتگرد می‌چرخد. در شکل اول، اشتراک لوزی و مربع سیاه است. در شکل دوم، قسمتی از لوزی که با مربع اشتراک ندارد، سیاه است. در شکل سوم، قسمتی از مربع که با لوزی اشتراک ندارد، سیاه است. بنابراین، در شکل چهارم، اشتراک لوزی و مربع باید سیاه باشد. بنابراین، شکل زیر، پاسخ مسئله است.

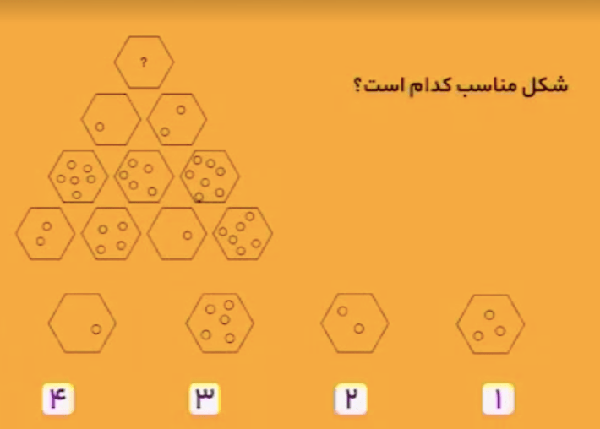
در سطر دوم (از پایین)، تعداد دایره‌های داخل هر شش‌ضلعی برابر است با مجموع تعداد دایره‌های دو شش‌ضلعی زیر آن.
در سطر سوم (از پایین)، تعداد دایره‌های داخل هر شش‌ضلعی برابر است با اختلاف تعداد دایره‌های دو شش‌ضلعی زیر آن.
در نتیجه، تعداد دایره‌های شش‌ضلعی بالای شکل باید برابر باشد با مجموع تعداد دایره‌های دو شش‌ضلعی‌ زیر آن. بنابراین، شکل زیر، پاسخ مسئله است.

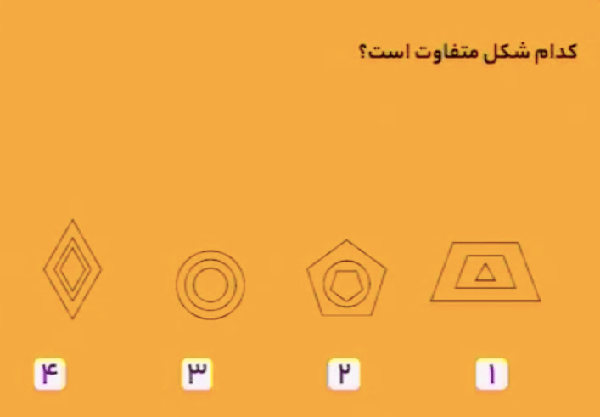
در همهٔ تصویرهای داده شده، به‌جز تصویر زیر، شکل بیرونی و شکل درونی تکراری هستند.