مسابقه تلویزیونی هوشیار – قسمت ۲

گزینهٔ ۱ درست است.

\[\begin{aligned}&{\color{red}8}\,{\color{blue}3}\quad{\color{red}6}\,{\color{blue}4}\quad{\color{red}4}\,{\color{blue}5}\quad{\color{red}?}\,{\color{blue}?}\\&{\color{green}9}\,{\color{purple}6}\quad{\color{green}6}\,{\color{purple}5}\quad{\color{green}3}\,{\color{purple}4}\quad{\color{green}?}\,{\color{purple}?}\end{aligned}\] دنبالهٔ قرمزرنگ با عدد \(8\) شروع می‌شود و هر عدد \(2\) واحد از عدد قبلی‌اش کمتر است.
دنبالهٔ آبی‌رنگ از عدد \(3\) شروع می‌‌شود و هر عدد \(1\) واحد از عدد قبلی‌اش بیشتر است.
دنبالهٔ سبزرنگ از عدد \(9\) شروع می‌شود و هر عدد \(3\) واحد از عدد قبلی‌اش کمتر است.
دنبالهٔ بنفش‌رنگ از عدد \(6\) شروع می‌‌شود و هر عدد \(1\) واحد از عدد قبلی‌اش کمتر است.
پس:
\[\begin{aligned}&{\color{red}8}\,{\color{blue}3}\quad{\color{red}6}\,{\color{blue}4}\quad{\color{red}4}\,{\color{blue}5}\quad{\color{red}2}\,{\color{blue}6}\\&{\color{green}9}\,{\color{purple}6}\quad{\color{green}6}\,{\color{purple}5}\quad{\color{green}3}\,{\color{purple}4}\quad{\color{green}0}\,{\color{purple}3}\end{aligned}\]

\[\begin{aligned}&3=1\times{\color{blue}2}+{\color{red}1}\\&11=3\times{\color{blue}3}+{\color{red}2}\\&47=11\times{\color{blue}4}+{\color{red}3}.\end{aligned}\] بنابراین، به‌جای علامت سؤال باید عدد \(239\) قرار بگیرد. زیرا:
\[239=47\times{\color{blue}5}+{\color{red}4}.\]

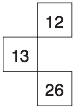
در هر سطر و هر ستون، شکل سوم از شکل‌های اول و دوم همان سطر یا ستون ساخته می‌شود. در شکل سوم هر سطر یا ستون، فقط خطوطی ظاهر می‌شوند که در هر دو شکل قبلی وجود دارند.
بنابراین، شکل زیر، پاسخ مسئله است.

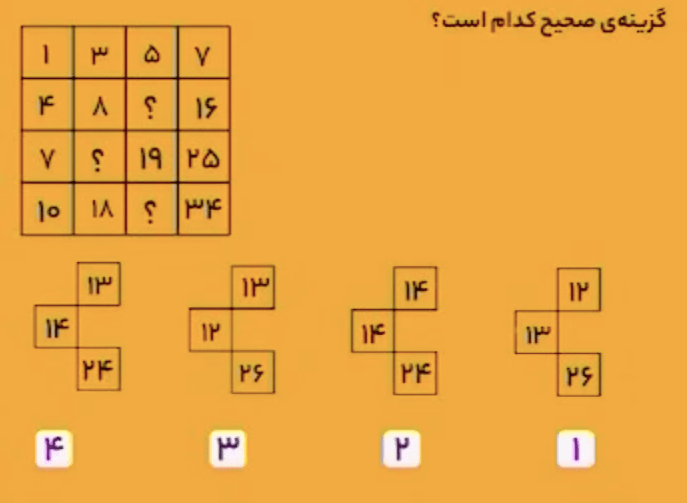
شکل شماره ۷ جواب مسئله است. تصویر آینه‌ای همهٔ شکل‌ها، به‌جز شکل شماره ۷، در جدول دیده می‌شود.

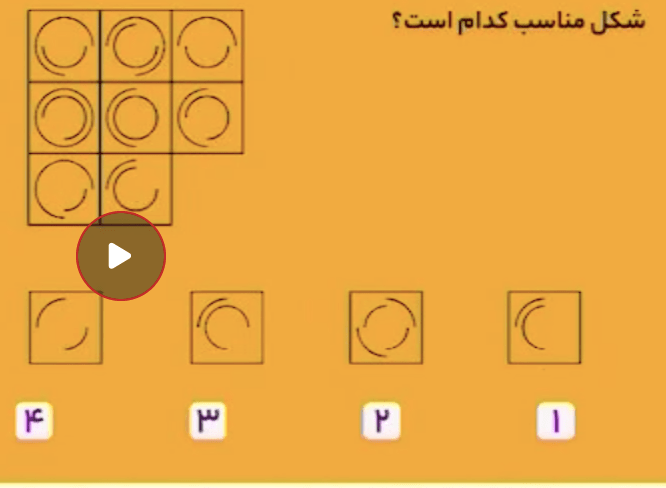
هر عدد نشان‌دهندهٔ تعداد اعداد مجاور (همسایه) خود به‌صورت افقی، عمودی، و مورب است.

اعداد سطرهای اول تا چهارم به‌ترتیب با روندِ \[+2,+4,+6,+8\] و اعداد ستون‌های اول تا چهارم به‌ترتیب با روندِ \[+3,+5,+7,+9\] تولید می‌شوند. بنابراین، شکل زیر، پاسخ مسئله است.

پاسخ، عدد \(8\) است.
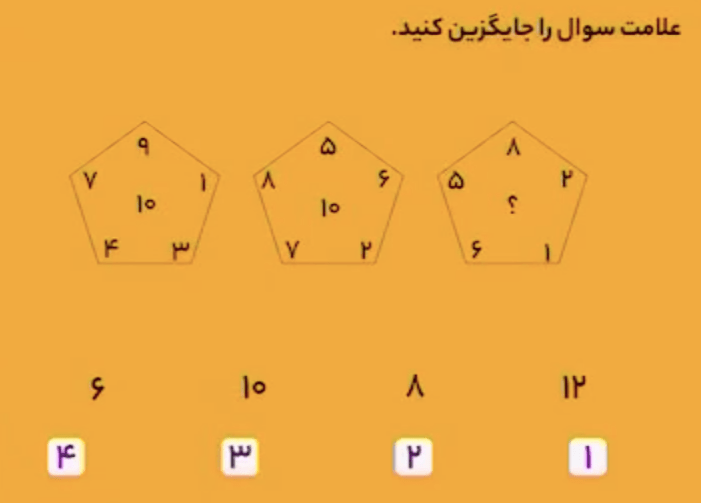
در هر شکل سه عدد بالایی را با هم و دو عدد پایینی را نیز با هم جمع کنید و حاصل آن‌ها را از هم کم کنید تا عدد مرکز شکل حاصل شود.
در شکل اول داریم:
\[(7+9+1)-(4+3)=10.\]
در شکل دوم داریم:
\[(8+5+6)-(7+2)=10.\]
بنابراین در شکل سوم داریم:
\[(5+8+2)-(6+1)=8.\]