مسابقه تلویزیونی هوشیار – قسمت ۲۵

مجموع کد ترتیب مستقیم و کد ترتیب معکوس هر حرف الفبا \(33\) است. کد حرف خواسته شده در ترتیب معکوس نصف کد حرف در ترتیب مستقیم است، یعنی باید عدد \(33\) را به نسبت \(1\) به \(2\) تقسیم کنیم.
برای اینکه \(33\) را به نسبت \(1\) به \(2\) تقسیم کنیم، ابتدا \(33\) را به \(3\) دستهٔ مساوی تقسیم می‌کنیم:
\[33\div3=11.\] حالا باید این \(3\) دسته را به نسبت \(1\) به \(2\) تقسیم کنیم؛ یعنی:
\[\begin{aligned}&11\times1=11,\\&11\times2=22.\end{aligned}\]
پس حرف مورد نظر بیست‌ودومین حرف الفبا، یعنی ‌«غ» است.

اگر چهار مربع \(2\times2\) گوشهٔ مربع \(4\times4\) را در نظر بگیریم، مربع‌های \(2\times2\) مقابل هم باید یکسان باشند.

بنابراین، شکل زیر، قسمت حذف شده است.

اصل سؤال به صورت زیر است:
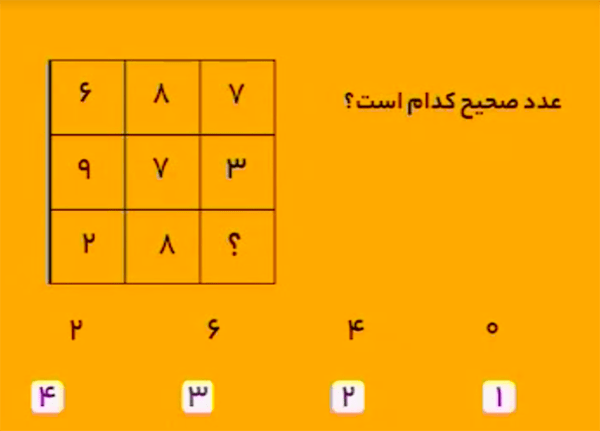
در جدول زیر، رابطه‌ای که بین نُه عدد سمت چپ جدول برقرار است، بین نهُ عدد سمت راست جدول نیز برقرار است. به‌جای علامت سؤال چه عددی باید قرار داد؟

پاسخ، عدد ۶ است.
در سمت چپ جدول،‌ هر سطر را یک عدد سه رقمی در نظر بگیرید. دراین‌صورت مجموع عدد سطر اول و عدد سطر سوم برابر است با عدد سطر دوم:
\[498+379=877\]

پاسخ، گزینهٔ ۴ است.

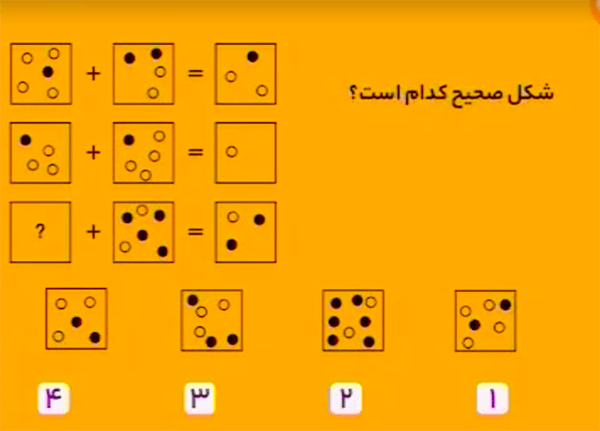
در هر سطر:
تعداد دایره‌های سفیدِ مربع سمت راستِ تساوی، برابر است با اختلاف بین دایره‌های سفیدِ مربع‌های سمت چپِ تساوی،
و تعداد دایره‌های سیاهِ مربع سمت راستِ تساوی، برابر است با اختلاف بین دایره‌های سیاهِ مربع‌های سمت چپِ تساوی.

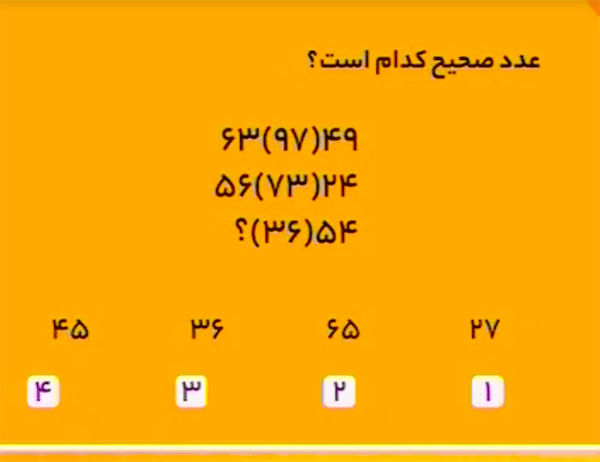
پاسخ، عدد 27 است.

در سطر اول هریک از اعداد چپ و راست (63 و 49) را بر 7 تقسیم کنید و حاصل‌ها را به‌هم بچسبانید تا عدد داخل پرانتز را بسازید.
در سطر دوم هریک از اعداد چپ و راست (56 و 24) را بر 8 تقسیم کنید و حاصل‌ها را به‌هم بچسبانید تا عدد داخل پرانتز را بسازید.
در سطر سوم باید هریک از اعداد چپ و راست را بر 9 تقسیم کنیم.

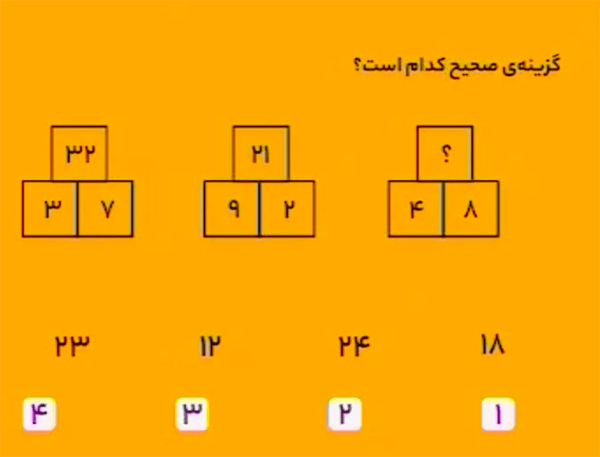
پاسخ عدد ۱۸ است.

حاصل‌ضرب دو عدد پایینیِ هر شکل، در بالا نوشته شود؛ البته نه در بالای همان دو عدد!

پاسخ، گزینهٔ زیر است.

شکل داده شده، یک مربعِ چهاردرچهار است. خانه‌های سطر اول این مربعِ چهاردرچهار با پاره‌خط‌هایی در چهار سطح پر شده است که این پاره‌خط‌ها را به‌ترتیب (از چپ به راست) سطح ۱، سطح ۲، سطح ۳، و سطح ۴ می‌نامیم. به‌این ترتیب، در خانه‌های سطر دوم، به‌ترتیب (از چپ به‌ راست) پاره‌خط‌های سطح ۲، سطح ۳، سطح ۴، و سطح ۱ وجود دارد.

قانون جدول این است که در خانه‌های هر سطر و هر ستون، پاره‌خط‌های هر سطح دقیقاً یکبار ظاهر شوند.

می‌توان مسئله را به‌صورت زیر مطرح کرد:
اعداد ۱، ۲، ۳، و ۴ را طوری در یک جدول چهاردرچهار بچینید که هریک از این اعداد، در هر سطر و هر ستون، دقیقاً یکبار ظاهر شوند.
به چنین مربعی، مربع لاتین از مرتبهٔ ۴ می‌گویند. برای آشنایی بیشتر با مربع‌های لاتین، اینجا را ببینید.