مجموع کد ترتیب مستقیم و کد ترتیب معکوس هر حرف الفبا \(33\) است. کد حرف خواسته شده در ترتیب معکوس ده برابر کد حرف در ترتیب مستقیم است، یعنی باید عدد \(33\) را به نسبت \(1\) به \(10\) تقسیم کنیم.
برای اینکه \(33\) را به نسبت \(1\) به \(10\) تقسیم کنیم، ابتدا \(33\) را به \(11\) دستهٔ مساوی تقسیم میکنیم:
\[33\div11=3.\] حالا باید این \(3\) دسته را به نسبت \(1\) به \(10\) تقسیم کنیم؛ یعنی:
\[\begin{aligned}&3\times1=3,\\&3\times10=30.\end{aligned}\]
پس حروف مورد نظر سومین و سیامین حرف الفبا، یعنی «پ» و «و» است.
پاسخ، عدد ۴۲ است.
\[\begin{aligned}24+6\times 1&=30\\30+6\times 2&=42\\42+6\times 3&=60\\60+6\times 4&=84\\84+6\times 5&=114\end{aligned}\]
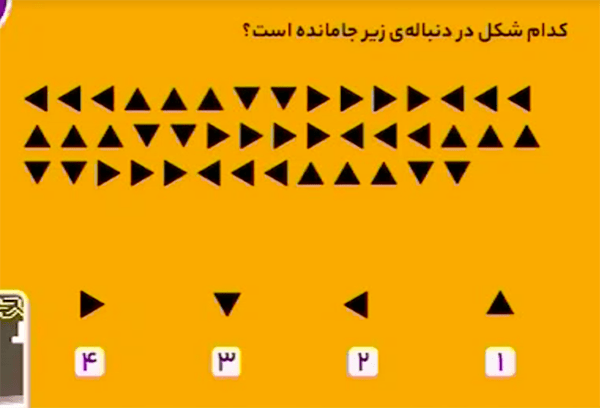
پاسخ، گزینهٔ ۴ است.
اگر گزینهٔ ۴ را در جای مشخص شده قرار دهیم، آنوقت در این دنباله، نمادهایی که در کادر قرمز قرار دارند، تکرار شدهاند.

پاسخ $27$ است.
عدد \(32\) از حاصلجمع عدد \(25\) با مجموع ارقام \(25\) بهدست میآید:
$$32=25+(2+5)$$
عدد \(27\) از کم کردن مجموع ارقام \(32\) از \(32\) بهدست میآید:
$$27=32-(3+2)$$
عدد \(36\) از حاصلجمع عدد \(27\) با مجموع ارقام \(27\) بهدست میآید:
$$36=27+(2+7)$$
پس عدد بعدی از کم کردن مجموع ارقام \(36\) از \(36\) بهدست میآید:
$$36-(3+6)=27$$
بنابراین، گزینهٔ ۱ درست است.
اعداد سطرهای اول تا سوم را یک عدد پنجرقمی در نظر میگیریم، عدد سطر چهارم حاصل جمع سه عدد سطرهای بالا است.
\[\begin{aligned}&27684\\+&12196\\+&25478\\[-7pt]&——–\\[-7pt]&65358\end{aligned}\]بنابراین، گزینهٔ ۱ درست است.
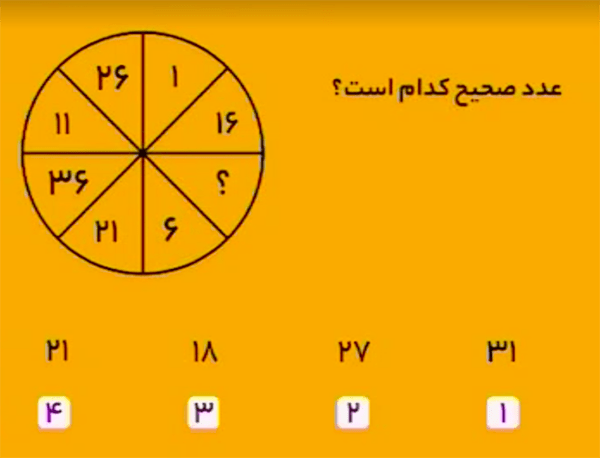
پاسخ $31$ است.
از $1$ شروع میکنیم و در هر مرحله سه خانه در جهت عقربههای ساعت جلو میرویم؛ رابطهٔ زیر ساخته میشود:
$$6=1+5$$ $$11=6+5$$ $$16=11+5$$ $$21=16+5$$ $$26=21+5$$ پس باید داشته باشیم:
$$?=26+5$$ و $$36=?+5$$
پس بهجای علامت سؤال باید عدد \(31\) را قرار داد.
بنابراین، گزینهٔ ۱ درست است.
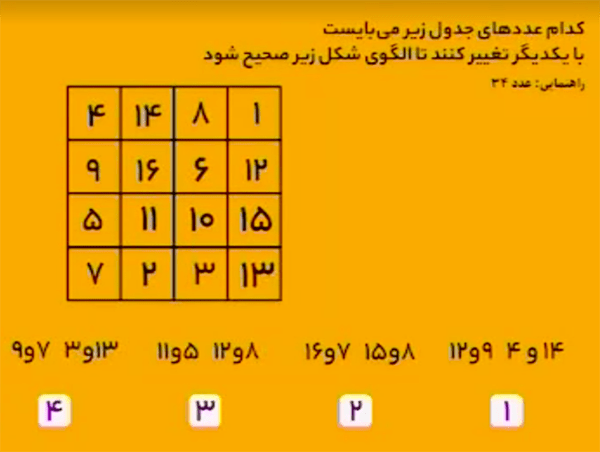
با توجه به راهنمایی سؤال و از اینکه با هیچ کدام از سطرها و ستونها نمیتوان عدد $34$ را ساخت، متوجه میشویم تغییر باید در تمام سطرها و ستونها اتفاق بیافتد. فقط تغییرات پیشنهادی گزینهٔ ۲ روی تمام سطرها و ستونها اثر میگذارد.
پاسخ $6814$ است.
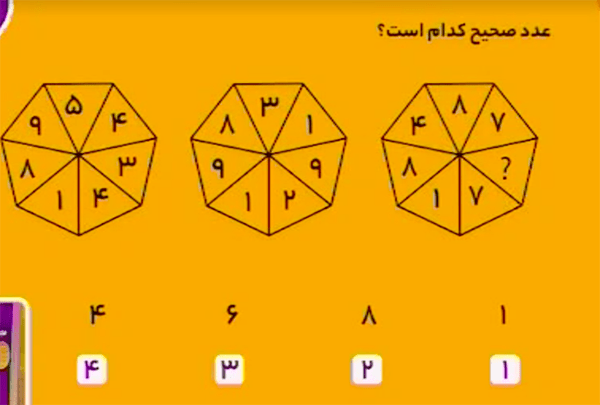
قانون تبدیل به این شکل است: جای دهگان و یکان هر عدد دو رقمی عوض میشود و مجموع ارقام سمت راست عدد نوشته میشود.
در شکل سمت چپ داریم:
$$89+54=143$$
در شکل میانی داریم:
$$98+31=129$$
و در شکل سمت راست داریم:
$$84+87=171$$
پس بهجای علامت سؤال باید عدد \(1\) را قرار داد.
بنابراین، گزینهٔ ۱ درست است.














ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️