در شکل سمت چپ داریم:
\[21\div3-4=3.\] در شکل میانی داریم:
\[56\div7-2=6.\] در شکل سمت راست داریم:
\[104\div8-3=10.\] بنابراین، گزینهٔ ۴ درست است.
\[\begin{aligned}&0.49\times{\color{red}1}=0.49\\&0.49\times{\color{red}2}=0.98\\&0.98\times{\color{red}3}=2.94\\&2.94\times{\color{red}4}=11.76\end{aligned}\] بنابراین، گزینهٔ ۴ درست است.
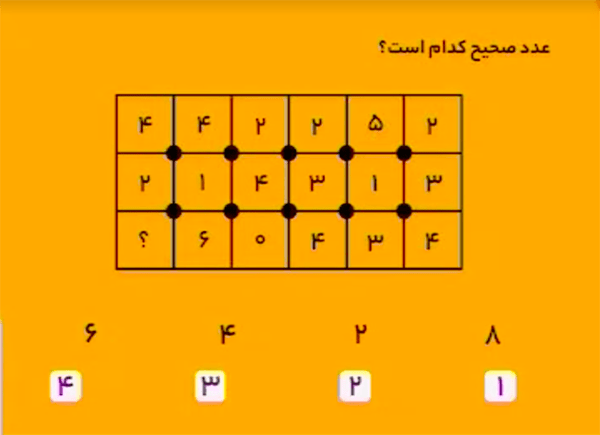
حاصلجمع چهار خانهٔ دور هر نقطهٔ سیاه برابر \(11\) است. پس اگر بهجای علامت سؤال، عدد \(2\) را قرار دهیم، داریم:
\[2+1+6+{\color{red}2}=11.\] بنابراین، گزینهٔ ۲ درست است.
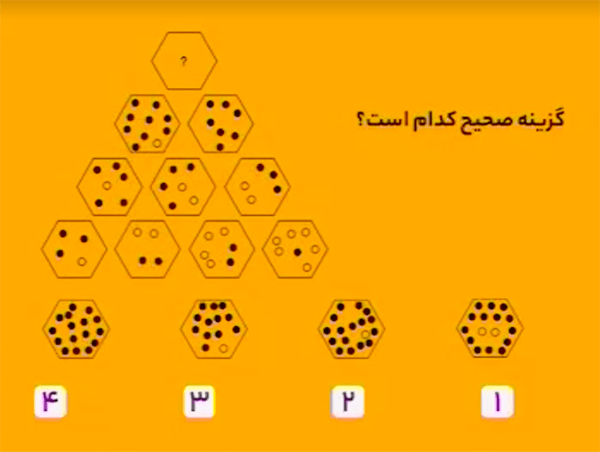
تعداد دایرههای توپر و توخالی هر ششضلعی، با قانونهای زیر، از دو ششضلعی زیرِ آن بهدست میآید:
\(\bullet\) تعداد دایرههای توپر هر ششضلعی برابر است با مجموع تعداد دایرههای توپر دو ششضلعی زیرِ آن.
\(\bullet\) تعداد دایرههای توخالی هر ششضلعی برابر است با اختلاف تعداد دایرههای توخالی دو ششضلعی زیرِ آن.
بنابراین، گزینهٔ ۲ درست است.
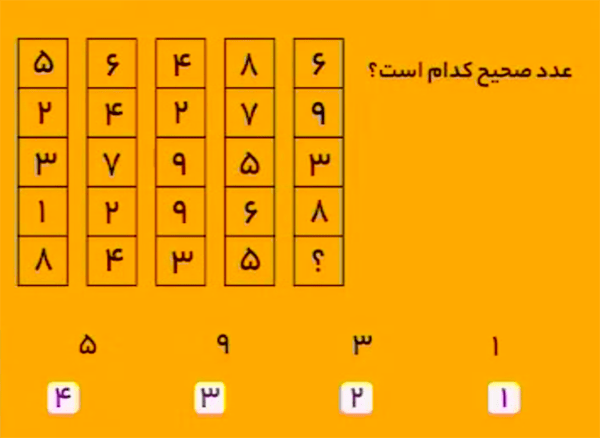
حاصلجمع اعداد ستونهای اول تا چهارم، بهترتیب از چپ به راست برابر است با:
\[19,23,27,31.\] این دنباله با عدد \(19\) شروع میشود و هر عدد \(4\) واحد از عدد قبلیاش بزرگتر است. پس مجموع اعداد ستون پنجم باید برابر \(35\) باشد. در نتیجه، بهجای علامت سؤال باید عدد \(9\) را قرار داد.
بنابراین، گزینهٔ ۳ درست است.
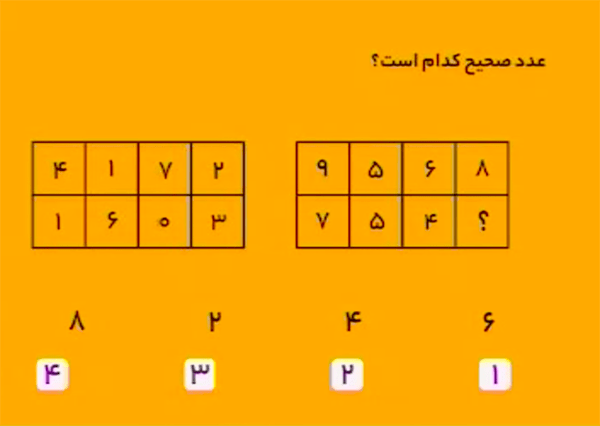
در هریک از جدولها، ابتدا اعداد سطر اول را با ترتیب برعکس بنویسید. برای مثال، در جدول سمت چپ، اگر \[4,1,7,2\] را با ترتیب برعکس بنویسیم، داریم: \[2,7,1,4\] سپس، از هریک از اعداد دنبالهٔ بالا \(1\) واحد کم کنید و آنها را در سطر دوم بنویسید:
\[1,6,0,3.\] اگر در جدول سمت راست هم همین کار را انجام دهیم، بهجای علامت سؤال باید
\[9-1=8\] را بنویسیم.
بنابراین، گزینهٔ ۴ درست است.
دنبالهٔ داده شده با عدد \(64\) شروع میشود.
عدد دوم از حاصلجمع ارقام عدد اول ساخته میشود:
\[6+4=10.\] عدد سوم اختلاف اعداد اول و دوم است:
\[64-10=54.\] عدد چهارم از مجموع ارقام عدد سوم بهدست میآید:
\[5+4=9.\] عدد پنجم اختلاف اعداد سوم و چهارم است:
\[54-9=45.\] و بقیهٔ اعداد دنباله نیز با همین قانون ساخته میشوند.
بنابراین، گزینهٔ ۴ درست است.
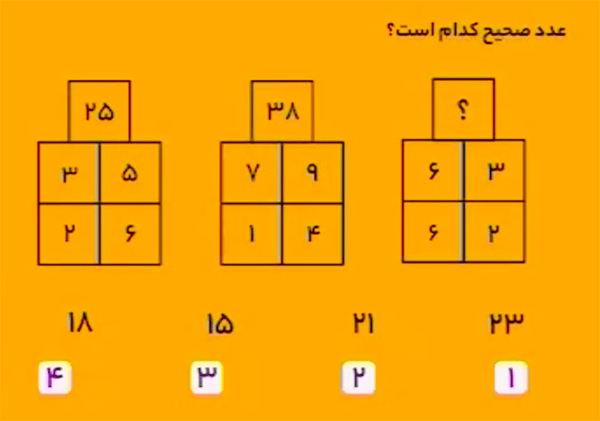
در جدول سمت چپ عدد بالایی با قانون زیر از عددهای پایینی ساخته میشود:
\[\begin{aligned}&3\times6=18\\&2+5=7\\&18+7=25.\end{aligned}\]
در جدول میانی نیز با همان قانون داریم:
\[\begin{aligned}&7\times4=28\\&1+9=10\\&28+10=38.\end{aligned}\]
پس در جدول سمت راست خواهیم داشت:
\[\begin{aligned}&6\times2=12\\&6+3=9\\&12+9=21.\end{aligned}\]
بنابراین، گزینهٔ ۲ درست است.
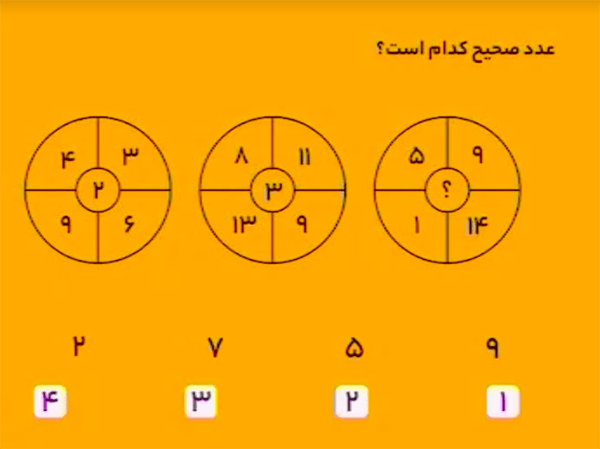
در دایرهٔ سمت چپ عدد وسط با قانون زیر از اعداد اطراف ساخته میشود:
\[\begin{aligned}&6\times4=24\\&3+9=12\\&24\div12=2\end{aligned}\]
در دایرهٔ میانی نیز با همان قانون داریم:
\[\begin{aligned}&9\times8=72\\&11+13=24\\&72\div24=3.\end{aligned}\]
پس در دایرهٔ سمت راست خواهیم داشت:
\[\begin{aligned}&14\times5=70\\&9+1=10\\&70\div10=7.\end{aligned}\] بنابراین، گزینهٔ ۳ درست است.












ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️