مجموع کد ترتیب مستقیم و کد ترتیب معکوس هر حرف الفبا \(33\) است. کد حرف خواسته شده در ترتیب معکوس دو برابر کد حرف در ترتیب مستقیم است، یعنی باید عدد \(33\) را به نسبت \(1\) به \(2\) تقسیم کنیم.
برای اینکه \(33\) را به نسبت \(1\) به \(2\) تقسیم کنیم، ابتدا \(33\) را به \(3\) دستهٔ مساوی تقسیم میکنیم:
\[33\div3=11.\] حالا باید این \(3\) دسته را به نسبت \(1\) به \(2\) تقسیم کنیم؛ یعنی:
\[\begin{aligned}&11\times1=11,\\&11\times2=22.\end{aligned}\]
پس حروف مورد نظر یازدهمین و بیستودومین حرف الفبا، یعنی «ذ» و «غ» است.
اصل متن به شکل زیر است:
انسان، چه بخواهد و چه نخواهد، به آن دلیل که دل به محدودیتهایش خوش نمیکند، به همان دلیل که کمال را میطلبد، به همان دلیل که هرجا گمان کرد محدودیتی در مقابلش سدی ایجاد کرده است، بدونِ درنگ، «چرا»ییِ آن محدودیت را جویا میشود، در نقطهای از مسیر زندگی خویش، از هستی خود و چرایی آن نیز پرسش میکند. آنجا که انسان به واقع از «خویش» پرسش میکند، آن لحظهایست که پاسخ برای او در حالی که بسیار آسان است، بسیار مشکل نیز میباشد.
بنابراین، گزینهٔ ۱ درست است.
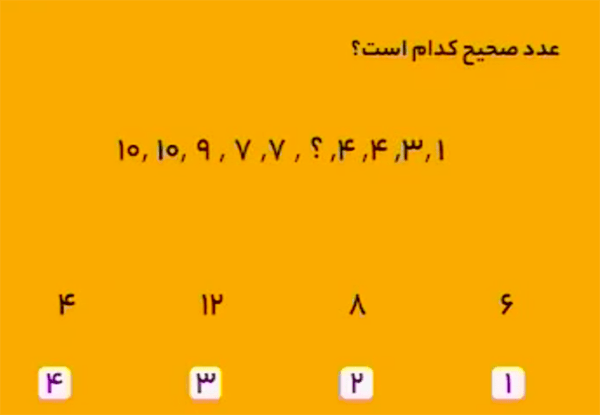
پاسخ، عدد ۶ است.
اعداد دنباله با روش زیر تولید شدهاند.
\[\begin{aligned}10-0&=10\\10-1&=9\\9-2&=7\\7-0&=7\\7-1&=6\\6-2&=4\\4-0&=4\\4-1&=3\\3-2&=1\end{aligned}\]
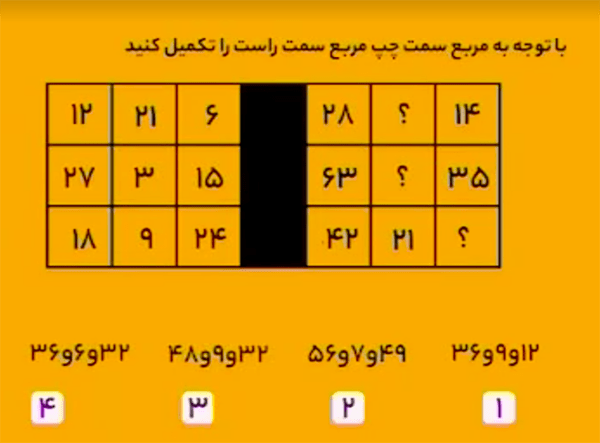
بهجای علامت سؤال سطر اول 49، بهجای علامت سؤال سطر دوم 7، و بهجای علامت سؤال سطر سوم 56 را باید قرار دهیم.
در نُه خانهٔ سمت چپِ جدول مضارب 3 و در نُه خانهٔ سمت راست جدول مضارب 7 قرار دارند. اگر اعداد را بهصورت زیر بنویسید، آنوقت بهسادگی تناظر بین اعداد سمت چپ و اعداد سمت راست جدول را میبینید.
بنابراین بهجای علامت سؤال سطر اول $7\times 7$، بهجای علامت سؤال سطر دوم $7\times 1$، و بهجای علامت سؤال سطر سوم $7\times 8$ را باید قرار دهیم.
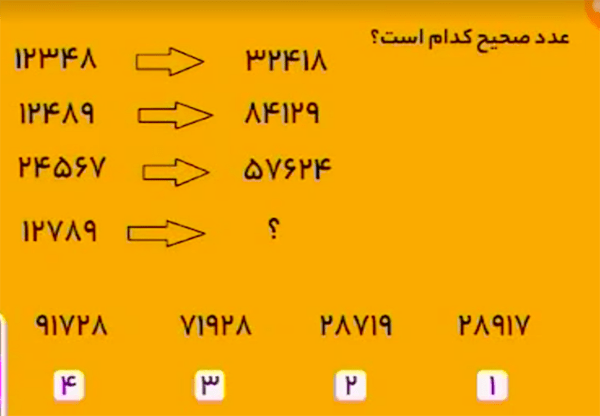
پاسخ، عدد 28917 است.
دو رقم از عدد سمت چپ انتخاب میکنیم بهطوریکه اگر با این دو رقم یک عدد دو رقمی بسازیم، رقمهای حاصلضرب این عدد دو رقمی در خودش، رقمهای دیگرِ عدد سمت چپ باشد. سپس، در سمت راست، ابتدا حاصلضرب عدد دو رقمی در خودش، و در ادامهٔ آن، عدد دو رقمی را مینویسیم.
\(\bullet\) در سطر اول، از عدد سمت چپ، رقمهای \(1\) و \(8\) را انتخاب میکنیم.
\[{\color{red}1}234{\color{red}8}\]
داریم:
\[18\times18={\color{blue}324}.\]
رقمهای \(3\)، \(2\)، و \(4\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}324}{\color{red}18}.\]
\(\bullet\) در سطر دوم، از عدد سمت چپ، رقمهای \(2\) و \(9\) را انتخاب میکنیم.
\[1{\color{red}2}48{\color{red}9}\]
داریم:
\[29\times29={\color{blue}841}.\]
رقمهای \(8\)، \(4\)، و \(1\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}841}{\color{red}29}.\]
\(\bullet\) در سطر سوم، از عدد سمت چپ، رقمهای \(2\) و \(4\) را انتخاب میکنیم.
\[{\color{red}24}567\]
داریم:
\[24\times24={\color{blue}576}.\]
رقمهای \(5\)، \(7\)، و \(6\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}576}{\color{red}24}.\]
\(\bullet\) در سطر چهام، از عدد سمت چپ، رقمهای \(1\) و \(7\) را انتخاب میکنیم.
\[{\color{red}1}2{\color{red}7}89\]
داریم:
\[17\times17={\color{blue}289}.\]
رقمهای \(2\)، \(8\)، و \(9\) در عدد سمت چپ موجود است. بنابراین، عدد سمت راست برابر است با:
\[{\color{blue}289}{\color{red}17}.\]
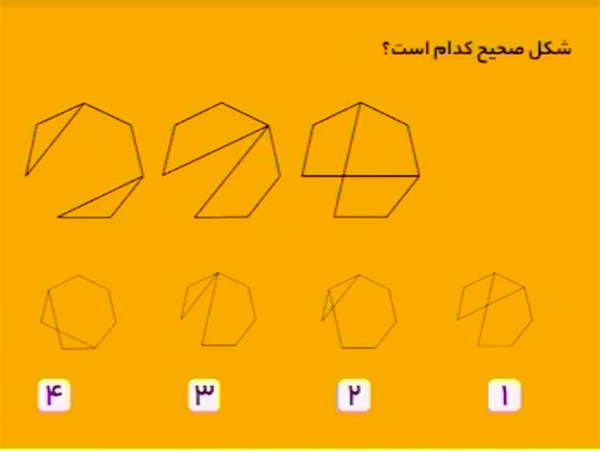
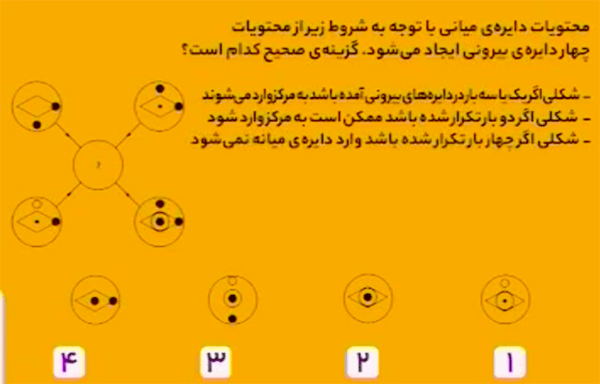
در تمام شکلها یک هفت ضلعی داریم که یک ضلع آن حذف شده است و دو قطری که از دو سر ضلع حذف شده میگذرد، رسم شده است. قطر بالایی در هر مرحله به صورت ساعتگرد یک رأس جابهجا میشود و قطر پایینی به صورت پادساعتگرد یک رأس جابهجا میشود. پس گزینهٔ ۴ صحیح است.
در چهار دایرهٔ کناری شکل لوزی چهار بار تکرار شده، پس طبق شرط سوم سؤال نباید در دایرهٔ میانی لوزی باشد. با توجه به گزینهها فقط گزینهٔ ۳ صحیح است.
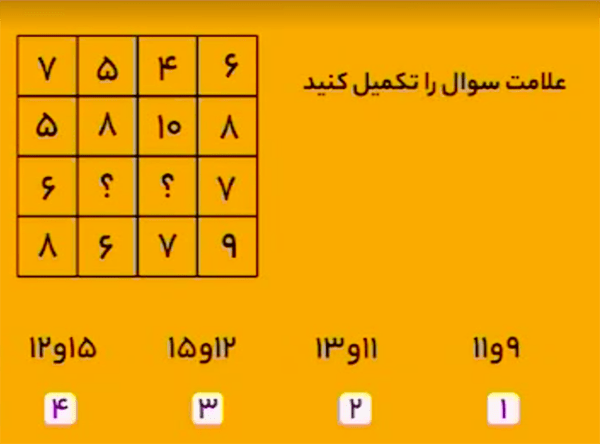
از گوشهٔ سمت راست بالای جدول شروع میکنیم و اعداد را به ترتیب پادساعتگرد مینویسم، دنبالهٔ زیر ساخته میشود:
$$6,4,5,7,5,6,8,6,7,9,7,8,10,8,?,?$$ قانون ساخت این دنباله به صورت زیر است:
$$-2,+1,+2,-2,+1,+2,-2,+1,+2,-2,+1,+2,-2,+1,+2$$
پس اعداد پانزدهم و شانزدهم دنبالهٔ بالا برابر است با:
$$8+1=9$$ $$9+2=11$$










ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️