مسابقه تلویزیونی هوشیار – قسمت ۵۲

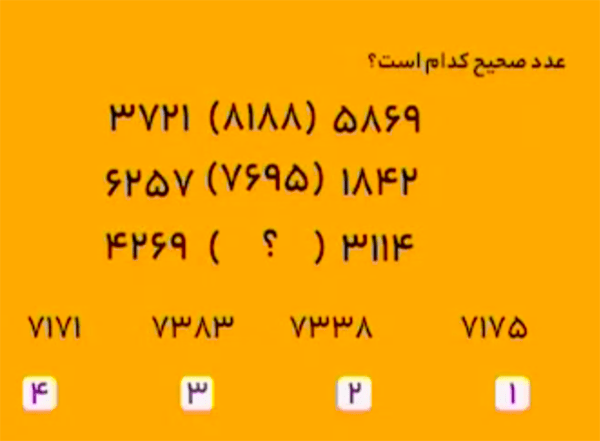
در هر شکل، چهار عدد اطراف را، مطابق آنچه در زیر گفته شده، به دو دسته تقسیم می‌کنیم.
در شکل سمت چپ، دسته اول \(42\) و \(73\)، و دسته دوم \(96\) و \(31\) هستند.
در شکل میانی، دسته اول \(27\) و \(76\)، و دسته دوم \(32\) و \(39\) هستند.
در شکل سمت راست، دسته اول \(36\) و \(84\)، و دسته دوم \(51\) و \(27\) هستند.

در هر شکل، عدد وسط از کنارهم قرار دادن «مجموع ارقام زوج اعداد دسته اول» و «مجموع ارقام فرد دسته دوم» به‌دست می‌آید.
در شکل سمت چپ، مجموع ارقام زوج اعداد دسته اول برابر است با:
\[4+2={\color{red}6}\] و مجموع ارقام فرد اعداد دسته دوم برابر است با:
\[9+3+1={\color{blue}13}.\]بنابراین، عدد وسط شکل سمت چپ برابر است با \({\color{blue}6}{\color{red}13}\).
در شکل میانی، مجموع ارقام زوج اعداد دسته اول برابر است با:
\[2+6={\color{blue}8}\] و مجموع ارقام فرد دسته دوم برابر است با:
\[3+3+9={\color{red}15}.\] بنابراین، عدد وسط شکل میانی برابر است با \({\color{blue}8}{\color{red}15}\).
در شکل سمت راست، مجموع ارقام زوج اعداد دسته اول برابر است با:
\[6+8+4={\color{blue}18}\] و مجموع ارقام فرد دسته دوم برابر است با:
\[5+1+7={\color{red}13}.\] بنابراین، عدد وسط شکل سمت چپ برابر است با \({\color{blue}18}{\color{red}13}\).
بنابراین، گزینهٔ ۳ درست است.

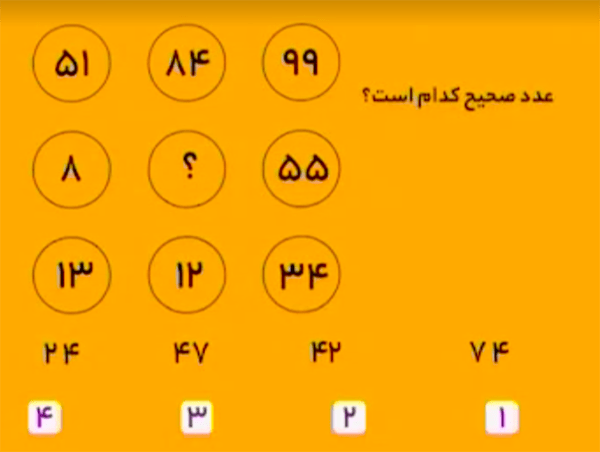
در سطر اول داریم:
\[99-51=48\] که اگر رقم‌های \(48\) را جابه‌جا کنیم، عدد میانی سطر اول، یعنی \(84\)، به‌دست می‌آید.
در سطر سوم داریم:
\[34-13=21\] که اگر رقم‌های \(21\) را جابه‌جا کنیم، عدد میانی سطر سوم، یعنی \(12\)، به‌دست می‌آيد.
در سطر دوم داریم:
\[55-8=47\] که اگر رقم‌های \(47\) را جابه‌جا کنیم، عدد میانی سطر دوم، یعنی \(74\)، به‌دست می‌آید.
بنابراین،‌ گزینهٔ ۱ درست است.

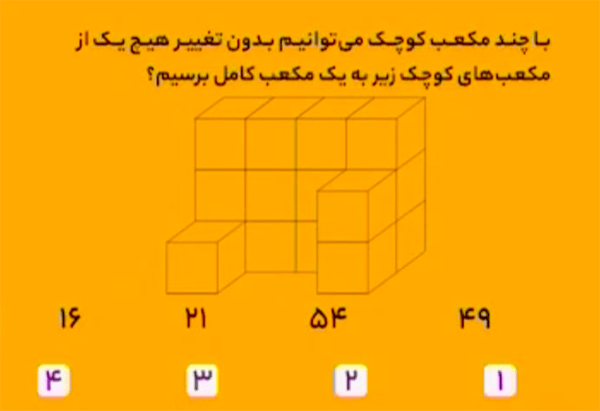
این شکل می‌تواند به یک مکعب \(4\times4\times4\) که از \(64\) مکعب واحد تشکیل شده است، تبدیل شود. چون در شکل داده شده \(15\) مکعب واحد وجود دارد، پس برای اینکه این شکل به یک مکعب کامل تبدیل شود باید
\[64-15=49\] مکعب واحد به آن اضافه کرد.

گزینهٔ ۱ درست است.

برای به‌دست آوردن عدد بعدی، هر عدد را با تک‌تک رقم‌هایش جمع می‌زنیم:
\[\begin{aligned}&59+5+9=73\\&73+7+3=83\\&83+8+3=94\\&94+9+4=107\\&107+1+0+7=115.\end{aligned}\] بنابراین، گزینهٔ ۳ درست است.

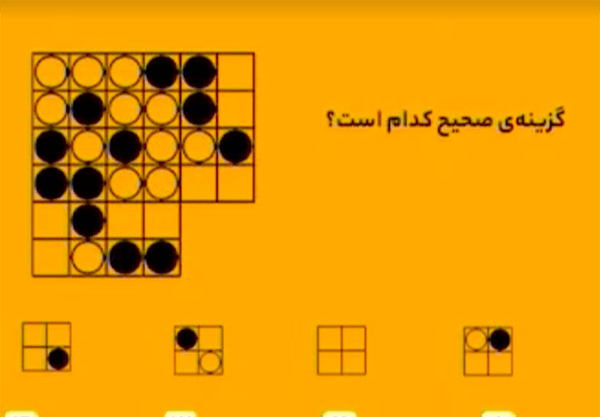
مطابق شکل بالا، جدول داده شده را به \(9\) قسمت تقسیم می‌کنیم. در هر سطر (از چپ به راست) و هر ستون (از بالا به پایین)، اگر مربع‌های آبی اول و دوم را روی‌هم بیندازیم، با قانون‌های زیر، مربع آبی سوم به‌دست می‌آید.
\(\bullet\) اگر دو دایرهٔ‌ تو خالی روی‌هم بیفتند، یک دایرهٔ توپر ساخته می‌شود.
\(\bullet\) اگر دو دایرهٔ توپر روی هم بیفتند، یک دایرهٔ توخالی ساخته می‌شود.
\(\bullet\) اگر یک دایره توخالی و یک دایرهٔ توپر روی‌هم بیفتند، یک خانهٔ خالی ساخته می‌شود.

بنابراین، گزینهٔ ۲ درست است.

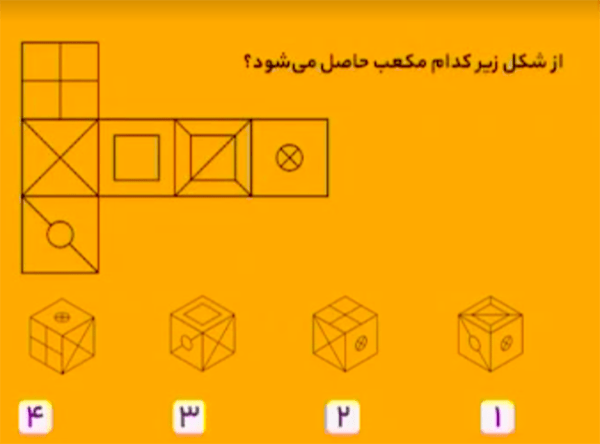
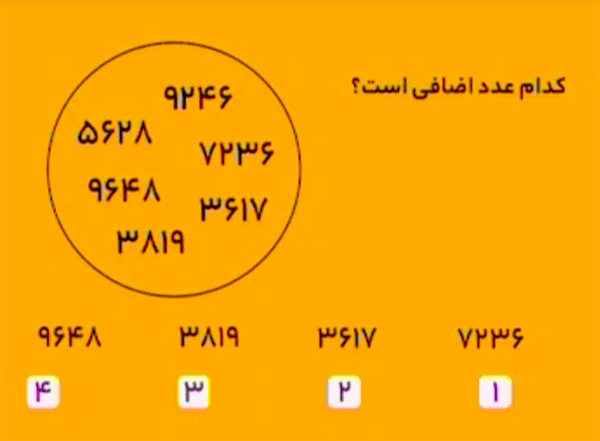
در هر عدد، اگر دورقم سمت راست را به‌عنوان یک عدد دورقمی درنظر بگیرید و آن را در \(2\) ضرب کنید، یک عدد دورقمی خواهید داشت که دورقم سمت چپ همان عدد است؛ به‌غیر از \(3617\).
\[\begin{aligned}&9246:\quad 46\times2=92\\&7236:\quad 36\times2=72\\&5628:\quad28\times2=56\\&9648:\quad48\times2=96\\&3819:\quad19\times2=38.\end{aligned}\] بنابراین، گزینهٔ ۲ درست است.

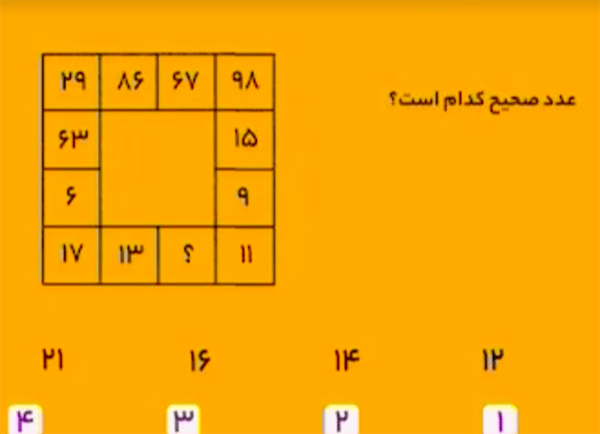
هر عدد از نیمهٔ بالای جدول را با عدد مقابلش در نیمهٔ پایین، به‌صورت زیر جفت می‌کنیم:
\[\begin{aligned}&63,9\\&29,11\\&86,?\\&67,13\\&98,17\\&15,6\end{aligned}\]
در هر سطر از اعداد بالا، حاصل‌جمع رقم‌های عدد سمت چپ برابر است با عدد سمت راست. پس، به‌جای علامت سؤال باید
\[8+6=14\] را قرار داد.
بنابراین، گزینهٔ ۲ درست است.

• یکان عدد میانی هر سطر برابر است با اختلاف یکان عدد سمت چپ و سمت راست آن سطر
• دهگان عدد میانی هر سطر برابر است با مجموع دهگان عدد سمت چپ و سمت راست آن سطر
• صدگان عدد میانی هر سطر برابر است با اختلاف صدگان عدد سمت چپ و سمت راست آن سطر
• هزارگان عدد میانی هر سطر برابر است با مجموع هزارگان عدد سمت چپ و سمت راست آن سطر

پس یکان، دهگان، صدگان، و هزارگان عدد میانی سطر سوم به‌ترتیب برابرند با:
\[\begin{aligned}&9-4=5\\&6+1=7\\&2-1=1\\&4+3=7.\end{aligned}\] در نتیجه عدد میانی سطر سوم برابر \(7175\) است.